投資の必要性については理解している。
しかし、「せっかく苦労して貯蓄したのでリスクは冒したくない」という方は多いのではないでしょうか?
それは、当然の感情です。



投資におけるリスクというのは平均的なリターンからのブレ幅のことを意味します。
このコンテンツでは、投資におけるリスクの考え方について以下の点を中心にお伝えしていきたいと思います。
■ 今回のポイント!
- リスクとは何なのか?
- リスクをどのように見るべきなのか?
- 株や投信等で数値化されるリスクリターンをどう理解するべきなのか?
尚、リスクを回避しつつ、投資で高いリターンを獲得するには、網羅的な金融知識(マネーリテラシー)が必要です。
老後2000万円問題などでも話題ですが、自分で資産を運用する力が本格的に求められる時代になりました。
「一度学べば一生使える知識」を獲得する方法として、「お金の学校」を活用するという選択肢も最近では注目を浴びています。
正しい資産形成の方法をこれから学ぶたいという方は、検討してみると良いでしょう。

目次
Contents
【イメージ編】投資におけるリスクとは?
まずは投資におけるリスクの意味をイメージで捉えていただきたいと思います。
リターンは過去から算出される平均リターン



例えば過去5年のリターンが3%というのは、過去5年間の値動きの平均年率リターン3%という意味です。
つまり過去5年の値動きを踏襲するならば、今年も平均的な値動きをすれば3%のリターンが見込めるということです。

リスクは値動きのブレ幅

例えばリターンが同じ企業Aと企業Bの株価の値動きを例にみていきましょう。
両社とも平均年率リターンは20%でしたが値動きは全くことなるものです。
| (平均年率20%成長) | 企業A | 企業B |
| 1年目 | 100 | 100 |
| 2年目 | 120 | 80 |
| 3年目 | 144 | 180 |
| 4年目 | 172.8 | 100 |
| 5年目 | 207.36 | 207.36 |
わかりやすく可視化すると以下となります。
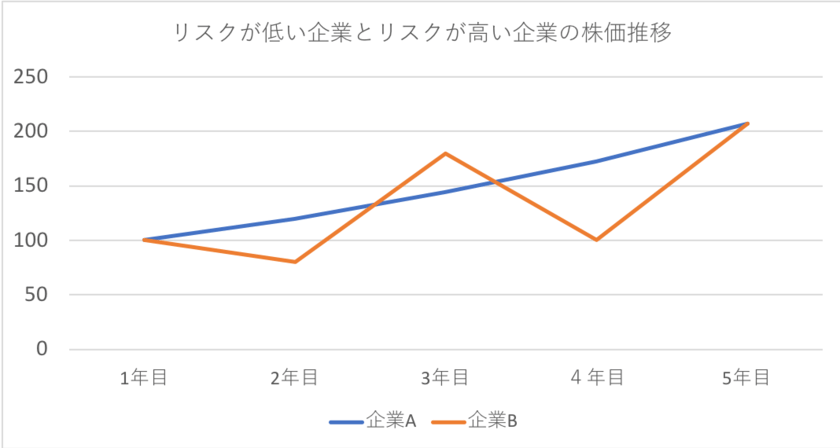


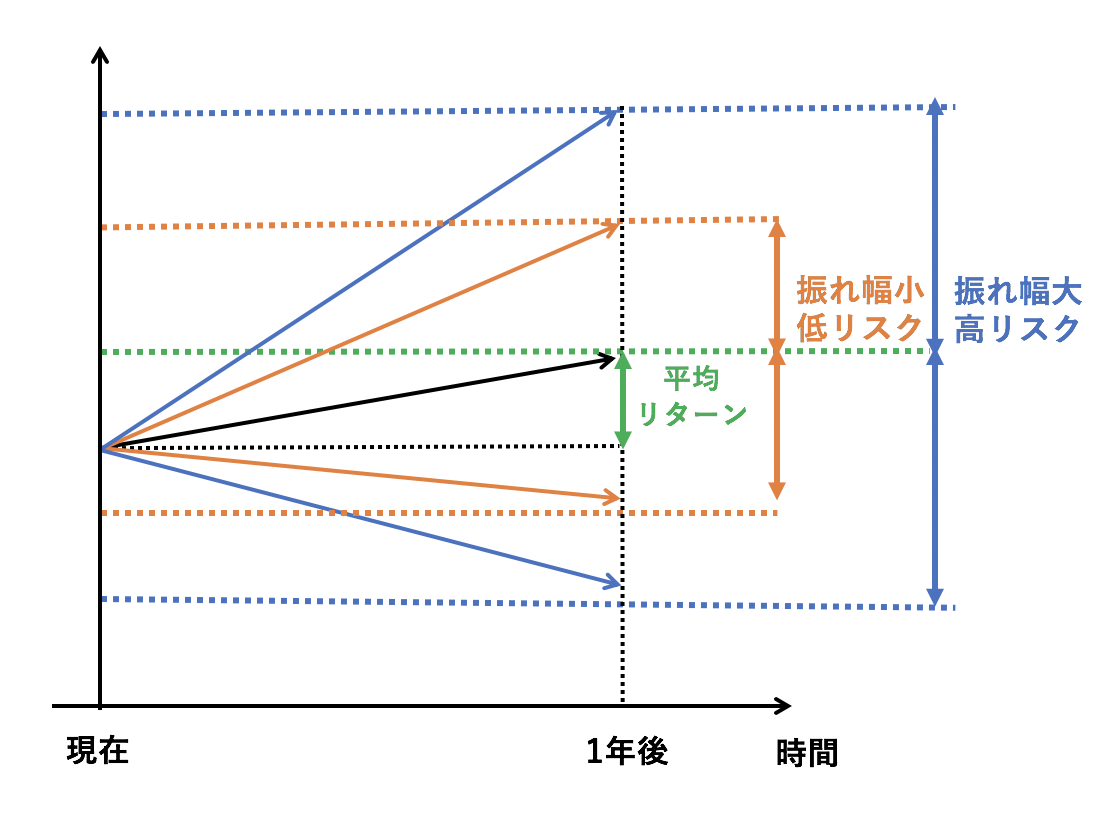
企業Aと企業Bの値動きに差を生んでいるのがリスクです。
企業Bの方がリスクが高いと感じるのは毎年度の価格の値動きのブレ幅が非常に大きいことに起因しています。
投資の世界では過去のリターンの平均からどれだけブレる可能性があるかを数値化したものをリスクと呼びます。
振れ幅が小さいことが過去の値動きから予想される場合を低リスク。
一方、振れ幅が大きいことが過去の値動きから予想される場合を高リスクといいます。
わかりやすくリスクが高い企業と低い企業の値動きをイメージ化すると以下の通りとなります。


以下平均年率リターンの計算方法については興味のある方のみご覧いただければと思います。
(目次に戻る)
〜コラム〜意外に難しい平均年率リターンの計算方法
平均年率リターンについては誤解されがちなので補足的に説明していきます。
例えば日経平均株価が以下のような推移を辿るとします。
(わかりやすいように数値は実際のものと異なります)
| 2015年 | 2016年 | 2017年 | 2018年 | 2019年 | |
| 日経平均 | 20,000 | 21,000 | 18,900 | 22,680 | 23,814 |
| 前年比 増加率 | – | +5% | ▲10% | +20% | +5% |



20,000円を5%で4年間運用した場合24,310円になってしまうのじゃ。
【計算式】
20,000円 × (1 +0.05 )^4 = 24,310円
平均年率5%では実際の2019年時点の23,814円と異なる日経平均になってしまうのです。



今回の場合に当てはめると、4.46%となります。

エクセルで (23,814/20,000)^(1/4) – 1をしてから100を掛けることで算出できます。
実際20,000円を年率4.46%で複利計算を行うことで23,814円となります。

それでは話を本題に戻してリスクについてより深く見ていきましょう。
(目次に戻る)
【統計学的意味編】投資におけるリスク(=標準偏差)とは
投信の目論見書を見ていただけばわかるのですがリスクは数値化されています。


数値化されているということは、計算によって算出されていることを意味します。
投資におけるリスクとは標準偏差のこと




標準偏差の求め方について気になる方は次項(標準偏差の計算法)をご覧ください。
標準偏差を自分で求める機会は稀ですので、標準偏差の意味するところを理解して頂きたいと思います。
統計学上標準偏差はσで表されるのですが、統計学的にσを図解したものが以下となります。
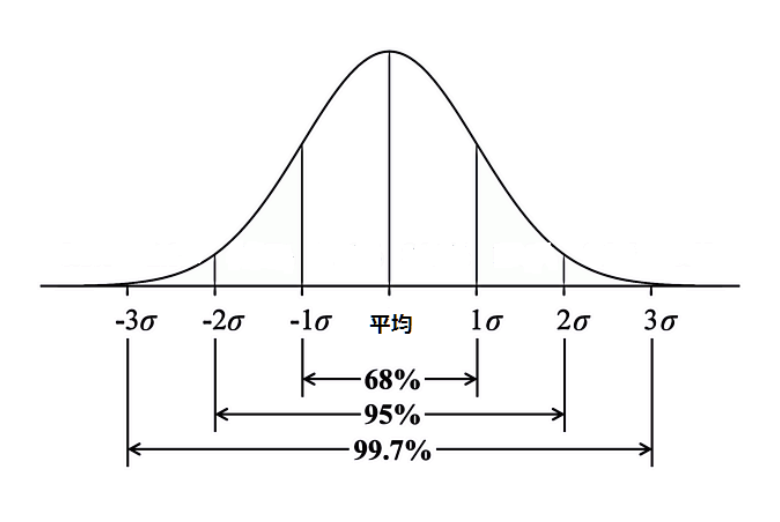

標準偏差を理解することで、「ある確率の中で収まる可能性のあるリターンのぶれ」を読み取ることができるようになります。
期待リターンから±1σにリターンが収束する可能性が68.2%
期待リターン±σに約68.2%の確率で1年後のリターンがおさまるということを意味します。
例えば平均リターンが10%でリスクが10%の銘柄が存在するとします。
すると、約68.2%の確率で1年後のリターンが平均リターン10%±10%に収まることを意味します。


期待リターンから±2σにリターンが収束する可能性が95%
期待リターン±2σに95%の確率で1年後のリターンがおさまるということを意味します。
先ほどの例を引き継ぐと、95%の確率で1年後のリターンが平均リターン10%±2×10%に収まることを意味します。


期待リターンから±3σにリターンが収束する可能性が99.7%
期待リターン±3σに99.7%の確率で1年後のリターンがおさまるということを意味します。
先ほどの例を引き継ぐと、99.5%の確率で1年後のリターンが平均リターン10%±3×10%に収まることを意味します。


リスクリターンが意味するところをさらに、体感してもらうために実際の例を用いながらお伝えしていきたいと思います。
その前に一旦標準偏差の求め方について軽く触れていきます。
(目次に戻る)
〜コラム〜簡単に標準偏差(=リスク)の計算法とエクセルでの求め方を解説
標準偏差については前項の意味するところを理解していただければ基本的には十分です。
以下算出方法については興味のある方だけご覧いただき、興味のない方はリスクリターンの見方まで飛ばしてください。
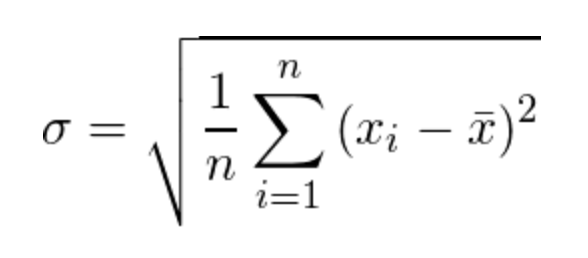
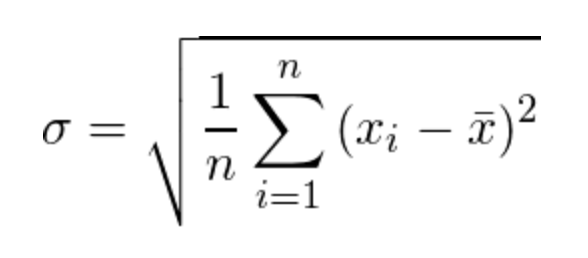


先ほどの例を用いて標準偏差を実際に計算する方法とエクセルで求める方法を見ていきましょう。
| 2015年 | 2016年 | 2017年 | 2018年 | 2019年 | |
| 日経平均 | 20,000 | 21,000 | 18,900 | 22,680 | 23,814 |
| 前年比 増加率 | – | +5% | ▲10% | +20% | +5% |
標準偏差(=リスク)を手計算で求める
まずは、どのような過程を経て算出されるのかを理解するために手計算で求める方法について紹介します。


STEP1. 前年比増加率の平均を求める
(+5%-10%+20%+5%) ÷ 4 = 5%
STEP2. 各年度の増加率と平均の差を求めて2乗する
1年目:(5%-5%)^2=0%
2年目:(▲10%-5%)^2=2.25%(※1)
3年目:(20%-5%)^2=2.25%(※2)
4年目:(5%-5%)^2=0%
(※1) 10%=0.1、5%=0.05のため
(-0.1-0.05)^2=0.0225=2.25%となります。
(※1) 20%=0.2、5%=0.05のため
(0.2-0.05)^2=0.0225=2.25%となります。
STEP3. STEP2を足し合わせて4で割る
(0%+2.25%+2.25%+0) / 4 =1.125%
STEP4. STEP3の平方根を求めて標準偏差が求まる
σ = √1.125% =10.6 %と求めることができます。
長いプロセスでしたね。




標準偏差(=リスク)をエクセルで簡単に求める
先ほどは手計算で4段階のステップにわけて求め方をお伝えしてきましたが、エクセルを用いれば簡単に算出することができます。
| A | B | C | D | E | F | |
| 1 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 | |
| 2 | 日経平均 | 20,000 | 21,000 | 18,900 | 22,680 | 23,814 |
| 3 | 前年比 増加率 | – | +5% | ▲10% | +20% | +5% |


=STDEVP(C3:F3)




(目次に戻る)
投資においてリスクリターンの意味するところ
では、本日最もご理解いただきたいリスクリターンについて意味することろお伝えしていきたいと思います。


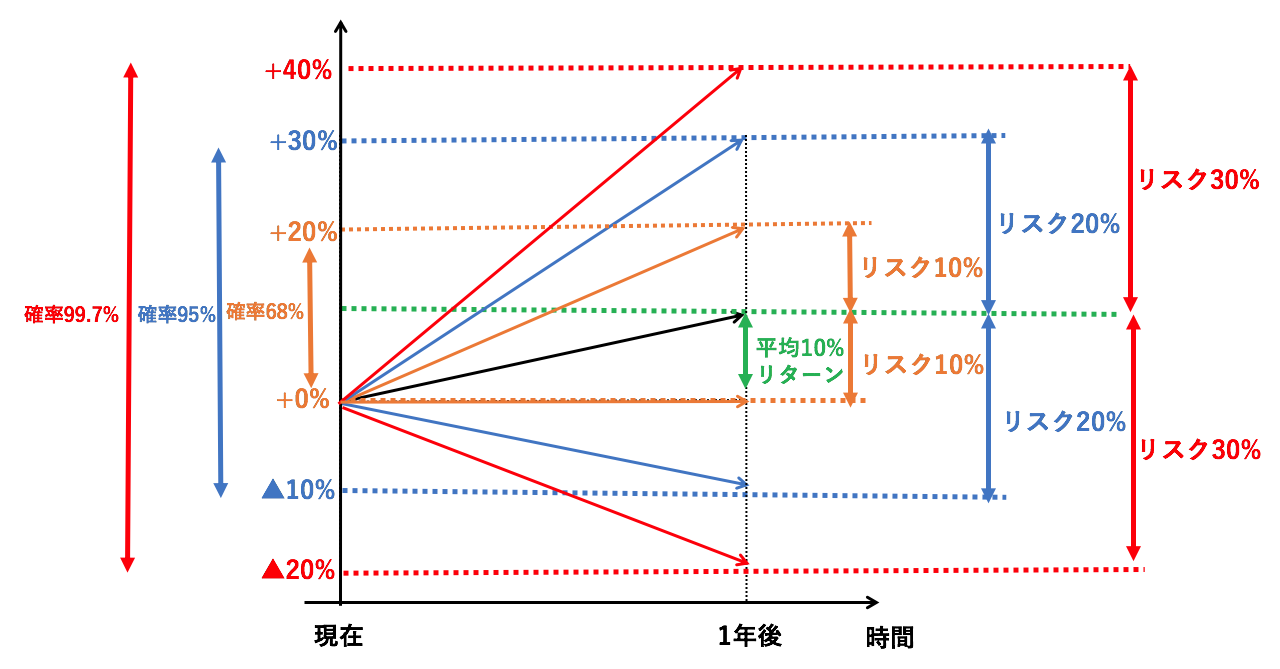

- 平均リターン10%から▲1σ(=▲10%) 〜 +1σ(=+10%)ブレる可能性が68%
- 平均リターン10%から▲2σ(=▲20%) 〜 +2σ(=+20%)ブレる可能性が95%
- 平均リターン10%から▲3σ(=▲30%) 〜 +3σ(=+30%)ブレる可能性が99.7%
つまり言い換えるとリターンが、以下の確率で以下の範囲で収まるということを意味しているのです。
- 0%(=平均10%-10%) 〜 20%(=平均10%+10%)に収まる可能性が約68%
- ▲10%(=平均10%-20%) 〜 30%(=平均10%+20%)に収まる可能性が約95%
- ▲20%(=平均10%-30%) 〜 40%(=平均10%+30%)に収まる可能性が約99.7%




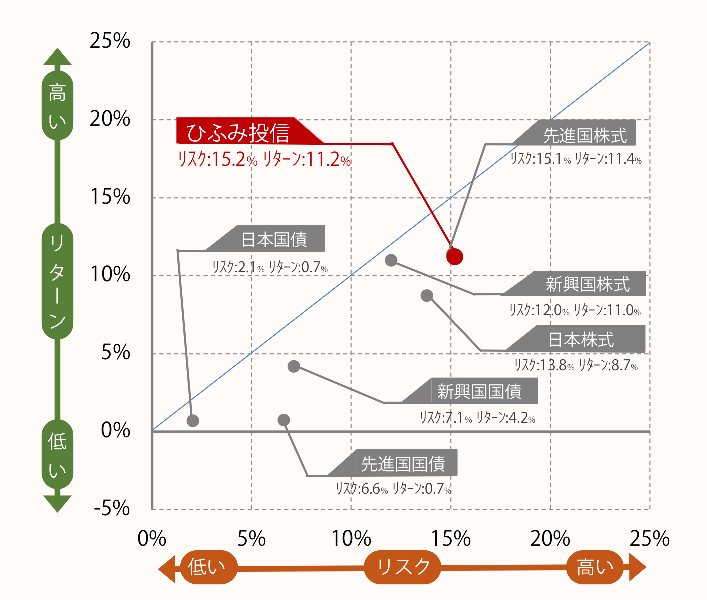

【ひふみ投信】(リターン11.2% リスク15.2%)
- ▲4%(=平均11.2%-15.2%) 〜26.4%(=平均11.2%+15.2%)に収まる可能性が約68%
- ▲19.2%(=平均11.2%-15.2%×2) 〜41.6%(=平均11.2%+15.2%×2)に収まる可能性が約95%
- ▲34.4%(=平均11.2%-15.2%×3) 〜56.8%(=平均11.2%+15.2%×3)に収まる可能性が約99.7%
【日本株式】(リターン8.7% リスク13.8%)
- ▲5.1%(=平均8.7%-13.8%) 〜22.5%(=平均8.7%+13.8%)に収まる可能性が約68%
- ▲18.9%(=平均8.7%-13.8%×2) 〜36.3%(=平均8.7%+13.8%×2)に収まる可能性が約95%
- ▲32.7%(=平均8.7%-13.8%×3) 〜50.1%(=平均8.7%+13.8%×3)に収まる可能性が約99.7%
【先進国株式】(リターン11.4% リスク15.1%)
- ▲3.7%(=平均11.4%-15.1%) 〜26.5%(=平均11.4%+15.1%)に収まる可能性が約68%
- ▲18.8%(=平均11.4%-15.1%×2) 〜41.6%(=平均11.4%+15.1%×2)に収まる可能性が約95%
- ▲33.9%(=平均11.4%-15.1%×3) 〜56.7%(=平均11.4%+15.1%×3)に収まる可能性が約99.7%




(目次に戻る)
リスクに対するリターンを表すシャープレシオという指標
最近はよくコストパフォーマンスという言葉が巷で使われるようになりました。
投資の世界においてコストパフォーマンスに相当する概念として使われている指標がシャープレシオです。


シャープレシオの意味と計算方法
シャープレシオは少ないリスクで高いリターンを狙いたいという投資家にとって有用な指標です。
リスク1単位あたりの超過リターンを測る指標で計算式は以下の通りです。
◼︎ シャープレシオの計算式:
シャープレシオ = (平均リターン – 無リスク資産収益率) /標準偏差(=リスク)




リターンから無リスク資産収益を差し引くことで、リスクをとって得られた収益を算出することができます。
何もリスクをとらなくても米国債に投資をすれば年率2%のリターンが得られたとします。
つまり、平均リターンが10%の投資商品でもリスクをとった結果得られるリターンは8%(=10%-2%)ということになります。
リスクをとった結果獲得した分をリスクである標準偏差でわることで、リスクに対するリターンを算出することができるのです。
シャープレシオが大きければ大きい程、少ないリスクで高いリターンを獲得できている銘柄ということになります。
シャープレシオの目安
シャープレシオの目安としては一般的に1を超えるのがよいとされています。


| シャープレシオの目安 | |
| 0.5-1.0 | 通常 |
| 1.0-2.0 | 優良 |
| 2.0以上 | 超優良 |
投資信託に関してはシャープレシオを日経新聞社がデータとして提供していますので参考にしましょう。
(目次に戻る)
まとめ
投資において下落する可能性の高さと思われがちな『リスク』。
しかし投資におけるリスクは価格の『ブレる幅』を表した指標で統計学上は標準偏差と言われています。
投資信託でリスクリターンと言われたら、平均的なリターンから確率的にどれだけブレる可能性があるのかという視点でリスクを見て頂けたらと思います。
今回の解説は、計算式も出てきて少し難解だったかもしれません。
しかし、投資の勉強を進め、金融知識が増えてくると、スムーズに理解ができるようになります。
リスクを的確に把握し、高いリターンを獲得するには、やはり勉強が必要です。
以下のコンテンツでは、株式投資を始める上で、効率的に学べる方法を紹介しています。
ぜひ参考にしてみてください。


また、投資の中でも株式投資は王道の選択肢になりますが、金投資や投資信託、ETFなど、世の中には様々な商品があります。
また、人それぞれ「リスク許容度」は異なります。
従い、自分にあった商品を選ぶにあたり、マネーリテラシーを高めることは今後の時代、ますます必須です。
「一度学べば一生使える知識」を獲得する方法として、「お金の学校」を活用するという選択肢もあるので、検討してみると良いでしょう。


以上、投資におけるリスク(=標準偏差)とは?株・投資信託のリスクリターンの意味・計算方法を理解しよう。…でした。